Computing √2 by additions alone
We’ve already seen a well-known algorithm to compute $\sqrt{2}$ to an arbitrary precision using Newton’s method in a previous post (see esp. footnote 1). Here is another approach discussed by Melzak.1 Let’s start with two positive integers $p_0$ and $q_0$, and the following recurrence relations, for $n = 0, 1, 2, \dots$:
$$ \begin{cases} p_{n+1} = p_n + 2q_n,\cr q_{n+1} = p_n + q_n \end{cases} $$
so that $p_n/q_n \to 2^{1/2}$. This can be demonstrated by noting that:
$$ p_{n+1}^2 - 2q_{n+1}^2 = -(p_n^2 - 2q_n^2) = \dots = (-1)^{n+1}(p_0^2 - 2q_0^2), $$
which implies that:
$$ \frac{p_{n+1}}{q_{n+1}} - 2^{1/2} = \frac{(-1)^{n+1}(p_0^2 - 2q_0^2)}{q_{n+1}(p_{n+1}+2^{1/2}q_{n+1})}. $$
Therefore, the sequence $p_0/q_0, p_1/q_1, \dots$ converges to $2^{1/2}$, as illustrated using the following Mathematica code:
values = RecurrenceTable[{x[n + 1] == x[n] + 2 y[n],
y[n + 1] == x[n] + y[n], x[0] == 1, y[0] == 1}, {x, y}, {n, 0,
20}];
xs = Apply[Divide, values, {1}];
ListPlot[xs, PlotRange -> All]
Compare the above to what would be obtained using the Newton derivative-based approach:
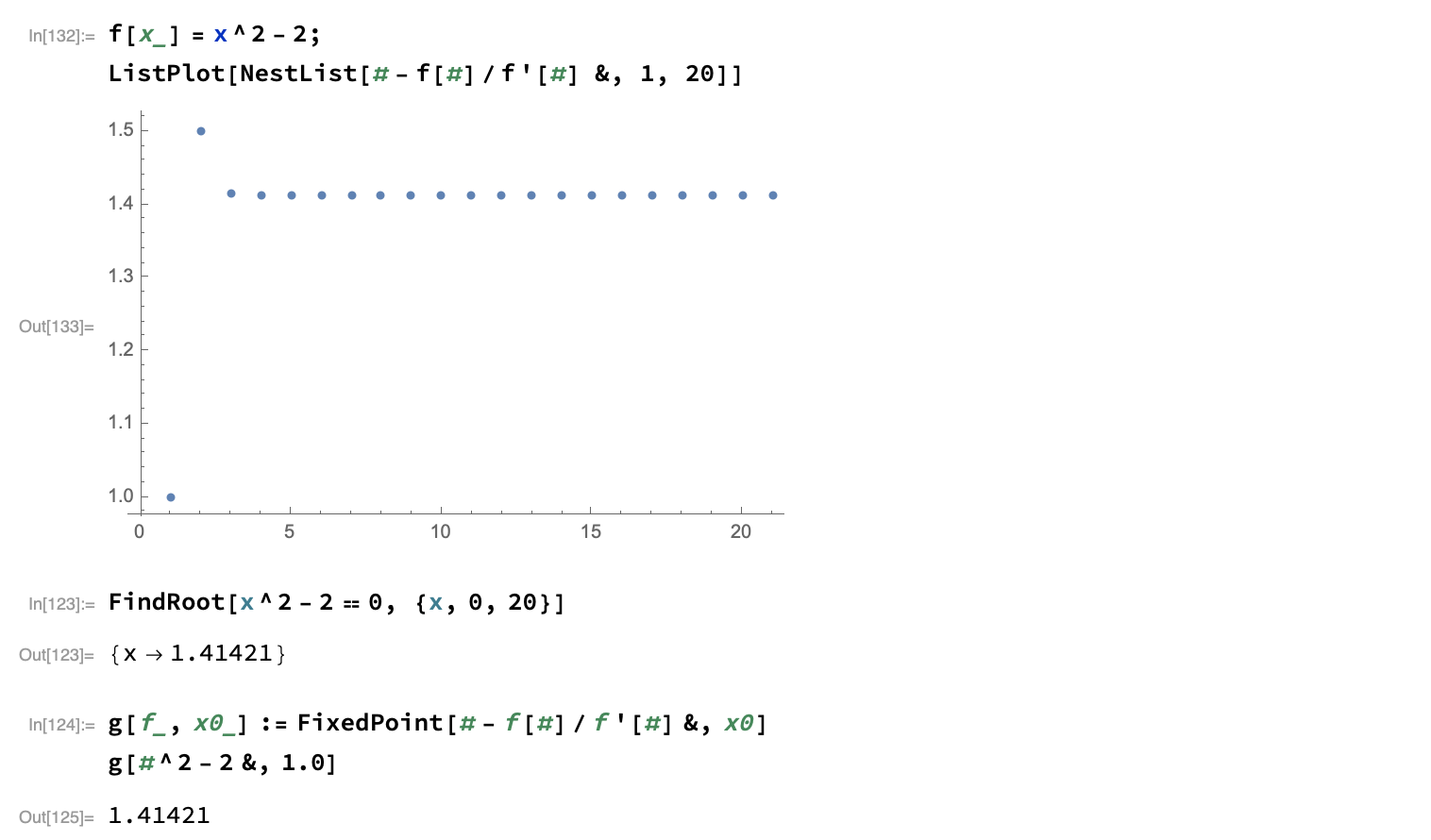
The convergence is quick.2 Note that the serie is alternating around $\sqrt{2}$, and we have:
$$ \left| \frac{p_n}{q_n} - 2^{1/2} \right| < \frac{1}{2} \left| \frac{p_n}{q_n} - \frac{p_{n-1}}{q_{n-1}} \right|, $$
suggesting a convenient stopping rule for any desired degree of accuracy.
Upon observing that the successive approximations $p_n/q_n$ are generated iteratively by means of two additions of integers only, Melzak then asks what other numbers can be similarly computed. To put in other words, let’s start with a series of integers $p_{10}, p_{20}, \dots, p_{k0}$, we require $p_{1n+1}, p_{2n+1},\dots, p_{kn+1}$ to be generable from $p_{1n}, p_{2n}, \dots, p_{kn}$ with a fixed number of additions only, i.e.:
$$ p_{in+1} = \sum_{j=1}^k c_{ij}p_{jn}, \qquad i = 1, 2, \dots, k;\quad n = 0, 1, 2, \dots $$
where the $c_{ij}$ are fixed integers. If a real irrational $x$ exists such that $x = \lim_{n\to\infty}p_{1n}/p_{2n}$, we call $x$ “computable by addition alone.” It turns out that $x$ is computable by additions alone if and only if it is algebric.
-
Z.A. Melzak, Companion to Concrete Mathematics, John Wiley & Sons, 1973. ↩︎
-
Newton-based mathods are known to have quadratic convergence. This is nicely illustrated in Numerical Methods That Usually Work, by Forman S. Acton (The Mathematical Association of America, 1990), pp. 54–55. The only requirement is that the derivative is not zero, or in other words that the root is isolated. The general algorithm for Newton’s method, for which the square-root algorithm is a special case, can be formulated as $x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)}$. This may be rewritten as $\varepsilon_{i+1} = \varepsilon_i - \frac{f_i}{f'i}$; When expanded as a Taylor series around the root $b$, we have $f(x_i) = f(b) + \varepsilon_i f'(b) + \varepsilon_i^2 \frac{f''(b)}{2} + \dots$, and $f'(x_i) = f'(b) + \varepsilon f''(b) + \dots$. Hence, $\varepsilon{i+1}$ can be rewritten as follows:
$$ \varepsilon_{i+1} = \varepsilon_i - \frac{\varepsilon_i f' + \varepsilon_i^2\frac{f''}{2} + \dots}{f' + \varepsilon_i f'' + \dots} = \frac{\varepsilon_i f' + \varepsilon_i^2 f'' + \dots - \varepsilon_i f' - \varepsilon_i^2\frac{f''}{2} - \dots}{f' + \varepsilon_i f'' + \dots}. $$
Finally, we have $\varepsilon_{i+1} \approx \varepsilon_i^2 \frac{f''}{2f'}$. ↩︎
